Горелка судного дня (сделает каждый): Без газа и электричества

Хорды в единичном круге и эллипсе

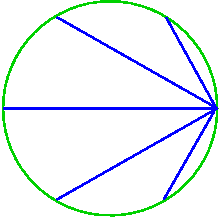
 Возьмите N равноудаленных точек на единичной окружности. Выберите одну из этих точек, затем проведите из нее хорды ко всем остальным точкам на окружности, как показано на рис. 1. Чему равно произведение длин этих хорд? Сюрприз: для N точек произведение равно N. Круто, да ?

Что будет, если мы рассмотрим подобную операцию с элипсом вместо круга?

Рассмотрим N равноотстоящих точек на единичной окружности, с точкой P=(1,0) в качестве одной из этих равноотстоящих точек, и проведем (N-1) хорды от P до каждой другой точки. В первой части мы видели, что произведение длин этих хорд равно N. Но что произойдет, если мы растянем этот круг так, чтобы он стал эллипсом?

Например, предположим, что мы рассматриваем единичный круг (с хордами, проведенными от P к N-1 равноотстоящим точкам на круге), и теперь масштабируем вертикальное направление на Sqrt[5], так что круг становится эллипсом, вытянутым по вертикали ( и точки, где хорды встречаются с эллипсом, больше не находятся на одинаковом расстоянии друг от друга вдоль эллипса). Обратите внимание, что хорды удлиняются при таком масштабировании. Чему равно произведение длин хорд?

Удивительно, но это всего в N раз больше N-го числа Фибоначчи!

Закон Бенфорда

 

Каков шанс, что случайное число начнётся с цифры «1»? Или с цифры «3»? Или с «7»? Если вы немного знакомы с теорией вероятности, то можете предположить, что вероятность — один к девяти, или около 11%.
Если же вы посмотрите на реальные цифры, то заметите, что «9» встречается гораздо реже, чем в 11% случаев. Также куда меньше цифр, чем ожидалось, начинается с «8», зато колоссальные 30% чисел начинаются с цифры «1». Эта парадоксальная картина проявляется во всевозможных реальных случаях, от количества населения до цен на акции и длины рек.
Физик Фрэнк Бенфорд впервые отметил это явление в 1938-м году. Он обнаружил, что частота появления цифры в качестве первой падает по мере того, как цифра увеличивается от одного до девяти. То есть «1» появляется в качестве первой цифры примерно в 30,1% случаев, «2» появляется около 17,6% случаев, «3» — примерно в 12,5%, и так далее до «9», выступающей в качестве первой цифры всего лишь в 4,6% случаев.
Чтобы понять это, представьте себе, что вы последовательно нумеруете лотерейные билеты. Когда вы пронумеровали билеты от одного до девяти, шанс любой цифры стать первой составляет 11,1%. Когда вы добавляете билет № 10, шанс случайного числа начаться с «1» возрастает до 18,2%. Вы добавляете билеты с № 11 по № 19, и шанс того, что номер билета начнётся с «1», продолжает расти, достигая максимума в 58%. Теперь вы добавляете билет № 20 и продолжаете нумеровать билеты. Шанс того, что число начнётся с «2», растёт, а вероятность того, что оно начнётся с «1», медленно падает.
Закон Бенфорда не распространяется на все случаи распределения чисел. Например, наборы чисел, диапазон которых ограничен (человеческий рост или вес), под закон не попадают. Он также не работает с множествами, которые имеют только один или два порядка.
Тем не менее, закон распространяется на многие типы данных. В результате власти могут использовать закон для выявления фактов мошенничества: когда предоставленная информация не следует закону Бенфорда, власти могут сделать вывод, что кто-то сфабриковал данные.

Елизавета Баварская - императрица Австрии. Рассказывает историк Наталия ...