Трехмерный аналог теоремы Пифагора. Теорема де Гюа

В 18-м столетии французский математик Жан Поль де Гюа де Мальв (1712 — 1785) открыл трехмерный аналог теоремы Пифагора.

Если в шестиграннике есть прямой угол, такой, как в кубе, то квадрат площади поверхности, противостоящей углу, равна сумме квадратов площадей трех других граней.


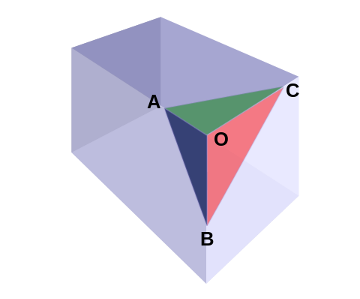
 Квадрат площади треугольника ABC равна сумме квадратов площадей треугольников ABO, ACO и BCO.