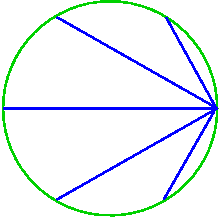
Возьмите N равноудаленных точек на единичной окружности. Выберите одну из этих точек, затем проведите из нее хорды ко всем остальным точкам на окружности, как показано на рис. 1. Чему равно произведение длин этих хорд? Сюрприз: для N точек произведение равно N. Круто, да ?
Рассмотрим N равноотстоящих точек на единичной окружности, с точкой P=(1,0) в качестве одной из этих равноотстоящих точек, и проведем (N-1) хорды от P до каждой другой точки. В первой части мы видели, что произведение длин этих хорд равно N. Но что произойдет, если мы растянем этот круг так, чтобы он стал эллипсом?
Например, предположим, что мы рассматриваем единичный круг (с хордами, проведенными от P к N-1 равноотстоящим точкам на круге), и теперь масштабируем вертикальное направление на Sqrt[5], так что круг становится эллипсом, вытянутым по вертикали ( и точки, где хорды встречаются с эллипсом, больше не находятся на одинаковом расстоянии друг от друга вдоль эллипса). Обратите внимание, что хорды удлиняются при таком масштабировании. Чему равно произведение длин хорд?
Удивительно, но это всего в N раз больше N-го числа Фибоначчи!

Комментариев нет:
Отправить комментарий